doi: 10.56294/mw2024.588
ORIGINAL
A comprehensive study on improving time series forecasting precision
Un estudio exhaustivo sobre la mejora de la precisión de la previsión de series temporales
Mattukoyya Suhas Sahay1 *, Sreeja Ganta1 *, Bonu Naga Vamsi Vardhan1, Kamisetty Srilakshmi1 *
1Department of Computer Science and Engineering, Koneru Lakshmaiah Education Foundation. Guntur, Andhra Pradesh, India.
Cite as: Suhas Sahay M, Ganta S, Vamsi Vardhan BN, Srilakshmi K. A Comprehensive Study on Improving Time Series Forecasting Precision. Seminars in Medical Writing and Education. 2024; 3:.588. https://doi.org/10.56294/mw2024.588
Submitted: 05-12-2023 Revised: 24-02-2024 Accepted: 06-05-2024 Published: 07-05-2024
Editor: PhD.
Prof. Estela Morales Peralta
![]()
Corresponding Author: Mattukoyya Suhas Sahay *
ABSTRACT
This paper presents a comprehensive study aimed at enhancing the precision of time series forecasting. The primary objective is to investigate various techniques and methodologies to improve the accuracy of forecasting models, thereby providing valuable insights for practitioners in diverse domains reliant on time series predictions. The methodology encompasses data preprocessing, feature engineering, model selection, parameter tuning, and ensemble methods. Through meticulous analysis and experimentation, key findings reveal the effectiveness of different approaches in enhancing forecasting precision. Notably, our research underscores the significance of proper data preprocessing and feature engineering in achieving superior forecasting accuracy. Moreover, comparative evaluations of diverse forecasting models shed light on their relative performance and suitability across different time series datasets. The conclusions drawn from this study offer practical recommendations for practitioners to adopt strategies that optimize forecasting precision. Additionally, the study identifies avenues for future research, particularly in exploring advanced ensemble techniques and addressing the challenges associated with non-stationary data. Overall, this research contributes to the ongoing discourse on improving time series forecasting accuracy and underscores its importance in decision-making processes across various domains.
Keywords: Time Series Forecasting; Forecasting Precision; Data Preprocessing; Feature Engineering; Model Selection; Parameter Tuning.
RESUMEN
Este documento presenta un estudio exhaustivo destinado a mejorar la precisión de la previsión de series temporales. El objetivo principal es investigar diversas técnicas y metodologías para mejorar la precisión de los modelos de previsión, proporcionando así valiosos conocimientos a los profesionales de diversos ámbitos que dependen de las predicciones de series temporales. La metodología abarca el preprocesamiento de datos, la ingeniería de características, la selección de modelos, el ajuste de parámetros y los métodos de conjunto. A través de un meticuloso análisis y experimentación, los principales hallazgos revelan la eficacia de diferentes enfoques para mejorar la precisión de las previsiones. En particular, nuestra investigación subraya la importancia del preprocesamiento adecuado de los datos y la ingeniería de características para lograr una precisión de pronóstico superior. Además, las evaluaciones comparativas de diversos modelos de pronóstico arrojan luz sobre su rendimiento relativo y su idoneidad en diferentes conjuntos de datos de series temporales. Las conclusiones extraídas de este estudio ofrecen recomendaciones prácticas para que los profesionales adopten estrategias que optimicen la precisión de los pronósticos. Además, el estudio identifica vías para futuras investigaciones, en particular en la exploración de técnicas avanzadas de conjuntos y en el abordaje de los desafíos asociados con los datos no estacionarios. En general, esta investigación contribuye al discurso en curso sobre la mejora de la precisión de la previsión de series temporales y subraya su importancia en los procesos de toma de decisiones en diversos ámbitos.
Palabras clave: Previsión de Series Temporales; Precisión de Previsión; Preprocesamiento de Datos; Ingeniería de Características; Selección de Modelos; Ajuste de Parámetros.
INTRODUCTION
In the realm of predictive analytics, time series forecasting stands as a vital tool for anticipating future trends and patterns based on historical data. It encompasses a wide array of applications across diverse domains, including finance, economics, meteorology, and beyond. Understanding the intricacies of time series forecasting is crucial for making informed decisions and strategic planning in various sectors. This introduction aims to provide a foundational understanding of time series forecasting, highlighting its significance and relevance in today's data-driven world.(1)
Significance of Improving Precision in Time Series Forecasting
Enhancing the precision of time series forecasting holds paramount importance in contemporary decision-making processes. The ability to accurately predict future trends and patterns enables organizations to optimize resource allocation, minimize risks, and capitalize on emerging opportunities. Improved precision not only fosters better-informed strategic planning but also enhances operational efficiency and competitiveness in dynamic markets. Moreover, precise forecasting aids in mitigating potential losses, enhancing customer satisfaction, and fostering sustainable growth. In essence, the quest for precision in time series forecasting underscores its pivotal role as a cornerstone for driving innovation and achieving strategic objectives in today's fast-paced and data-driven environment.
Research Problem Statement
The research aims to address the challenge of enhancing the precision of time series forecasting methods. Despite advancements in forecasting techniques, achieving high accuracy remains a persistent challenge, particularly in domains where small deviations can have significant implications. The problem lies in the intricate nature of time series data, characterized by complex patterns, irregularities, and inherent uncertainties. Consequently, existing forecasting models often struggle to capture the nuances of such data, leading to suboptimal predictions and decision-making outcomes. Therefore, the research endeavors to identify effective strategies and methodologies to improve the precision of time series forecasting, thereby providing actionable insights for practitioners across various domains.
Objectives of the Study
The primary objective of this study is to comprehensively investigate and evaluate techniques aimed at improving the precision of time series forecasting. Specifically, the study seeks to achieve the following objectives:
· Evaluate various data preprocessing methods to enhance the quality and consistency of time series data.
· Explore innovative approaches for feature engineering to extract relevant patterns and trends from time series datasets.
· Compare and analyze different forecasting models, including traditional statistical methods, machine learning algorithms, and deep learning architectures.
· Investigate strategies for parameter tuning to optimize the performance of forecasting models.
· Assess the effectiveness of ensemble methods in combining multiple forecasting models to improve overall accuracy.
· Provide practical recommendations for practitioners to enhance the precision of time series forecasting in real-world applications.
Overview of the Paper Structure
This paper is structured to provide a comprehensive exploration of techniques and methodologies aimed at enhancing the precision of time series forecasting. It begins with an introduction that lays the groundwork by discussing the significance of time series forecasting and identifying the research problem. Following this, the paper presents a thorough review of existing literature, examining various approaches and methodologies used in time series forecasting.(2)
The methodology section outlines the research design and methodology adopted to achieve the objectives of the study. This includes discussions on data preprocessing, feature engineering, model selection, parameter tuning, and ensemble methods. Subsequently, the results section presents the findings of the study, including comparative analyses of different forecasting techniques and evaluations of forecasting models' performance.
The discussion and conclusion section interpret the results in the context of the research objectives, highlighting key insights and implications.(3) Additionally, this section outlines recommendations for practitioners and identifies areas for future research. Finally, the paper concludes with a summary of the key findings and the overall significance of the study in advancing the field of time series forecasting.
Literature review
Introduction to Literature Review
In the academic landscape, the literature review stands as a cornerstone of research endeavors, serving as a vital component in the formulation and execution of scholarly investigations. Its significance lies in its ability to provide researchers with a comprehensive understanding of existing knowledge, theories, and findings relevant to the chosen research topic. By synthesizing and critically analyzing prior studies, the literature review offers invaluable insights that inform the development of research questions, methodology, and theoretical frameworks.
Moreover, the literature review plays a crucial role in contextualizing the current study within the broader academic discourse. It serves as a foundation upon which researchers can build their arguments, identify gaps in existing literature, and propose avenues for further inquiry. Through a meticulous examination of prior research, scholars gain a nuanced understanding of the research landscape, enabling them to contribute meaningfully to their field of study.
Historical Context of Time Series Forecasting
Time series forecasting has a rich history dating back centuries, evolving from rudimentary methods to sophisticated techniques informed by advancements in mathematics, statistics, and computer science. This section provides an overview of the historical development of time series forecasting methods, tracing its evolution through seminal works and key milestones in the field.
The origins of time series forecasting can be traced back to the early civilizations, where rudimentary methods such as simple moving averages were used to predict future trends based on past observations. However, it was not until the late 19th and early 20th centuries that more formalized approaches began to emerge.
One of the foundational works in time series analysis is the autoregressive (AR) model, introduced by Yule in 1927, which laid the groundwork for understanding the temporal dependencies present in time series data. Building upon this, Box and Jenkins proposed the autoregressive integrated moving average (ARIMA) model in the 1970s, which remains one of the most widely used methods for time series forecasting.(4)
In parallel, the field of econometrics made significant contributions to time series forecasting, particularly through the work of Granger and Newbold, who developed the concept of autoregressive conditional heteroskedasticity (ARCH) models for modeling volatility in financial time series data.
The advent of computational technologies in the latter half of the 20th century paved the way for more advanced forecasting techniques, including exponential smoothing methods, state-space models, and machine learning algorithms. Notable advancements during this period include the introduction of neural networks for time series forecasting by Werbos in the 1970s and the development of support vector machines (SVMs) by Vapnik in the 1990s.
In recent years, deep learning approaches, particularly recurrent neural networks (RNNs) and long short-term memory (LSTM) networks, have gained prominence for their ability to capture complex temporal dependencies in sequential data. These advancements have led to breakthroughs in areas such as natural language processing, speech recognition, and financial forecasting.(5)
Overall, the historical development of time series forecasting methods reflects a trajectory of innovation driven by interdisciplinary collaboration and technological advancements. By tracing the evolution of the field through seminal works and key milestones, we gain insight into the progression of techniques and the challenges that have shaped contemporary approaches to time series forecasting.
Classical Statistical Methods
Traditional time series forecasting techniques, such as ARIMA (AutoRegressive Integrated Moving Average), have long served as foundational tools in the field of forecasting. These methods rely on statistical principles to model and predict future values based on past observations. This section provides an overview of classical statistical methods, delving into their underlying principles, assumptions, strengths, and limitations.
At the heart of classical statistical methods is the ARIMA model, which combines three components: autoregression (AR), differencing (I), and moving average (MA). The autoregressive component captures the linear relationship between an observation and a lagged value of the series, while the moving average component models the relationship between an observation and a residual error from a moving average model. The integration component accounts for any trend or seasonality present in the data by differencing the series to achieve stationarity.(6)
One of the key strengths of classical statistical methods is their simplicity and interpretability. ARIMA models, for example, provide clear and intuitive parameters that can be easily understood and interpreted. Additionally, these methods are robust and well-suited for modeling stationary time series data with a linear trend or seasonal patterns.
However, classical statistical methods also have several limitations. They often assume linearity in the underlying data generating process, which may not hold true for complex or nonlinear relationships. Moreover, these methods may struggle to capture and model long-term dependencies or nonlinear patterns present in the data. Additionally, ARIMA models require the data to be stationary, which may necessitate pre-processing steps such as differencing.
Despite these limitations, classical statistical methods remain valuable tools in the forecasting toolkit, particularly for modeling simple time series data with clear trends and seasonality. Their interpretability and ease of implementation make them accessible to practitioners across various domains, providing a solid foundation for more advanced forecasting techniques.(7)
Figure 1. Frequency Distribution of Sample Data with 5 Bins
Machine Learning Approaches
Machine learning techniques have emerged as powerful tools for time series forecasting, offering a diverse range of algorithms and methodologies to model complex temporal patterns. This section provides an overview of machine learning techniques applied to time series forecasting, focusing on regression-based methods and tree-based algorithms.
Regression-based methods, such as linear regression and polynomial regression, are commonly used for time series forecasting tasks. These models leverage historical data to learn a mapping between input features and output values, allowing them to make predictions based on observed patterns. Regression models are characterized by their simplicity and interpretability, making them suitable for exploring linear relationships in time series data.
Tree-based algorithms, including decision trees, random forests, and gradient boosting machines (GBMs), have gained popularity for their flexibility and ability to capture non-linear relationships in data. Decision trees recursively partition the feature space into smaller subsets, while random forests aggregate predictions from multiple decision trees to improve accuracy and reduce overfitting. GBMs iteratively train weak learners to minimize prediction errors, resulting in powerful ensemble models capable of capturing complex interactions in time series data.
Machine learning models handle time series data by treating each observation as a data point with associated features and target values. Features may include lagged variables, trend indicators, seasonal components, or external factors relevant to the forecasting task. By learning patterns from historical data, machine learning models can generalize to make predictions for future time points.
One of the key advantages of machine learning approaches over classical methods is their ability to capture complex and non-linear relationships present in time series data. Unlike traditional statistical models, which may assume linear dependencies or stationary processes, machine learning models can adapt to the dynamic nature of time series data and extract patterns that may not be apparent through manual analysis.(8)
Prominent machine learning models used in time series forecasting include Random Forest, which excels at handling high-dimensional data and capturing interactions between variables, and Gradient Boosting Machines, known for their robustness and performance on structured datasets. These models have been successfully applied in various domains, including finance, healthcare, and energy, demonstrating their versatility and effectiveness in real-world forecasting tasks.
Introduction to Deep Learning Architectures
Deep learning has revolutionized time series forecasting by leveraging complex neural network architectures capable of capturing intricate temporal dependencies. Among these architectures, Recurrent Neural Networks (RNNs) and Long Short-Term Memory (LSTM) networks stand out for their effectiveness in handling sequential data.
Recurrent Neural Networks (RNNs)
RNNs are designed with recurrent connections, enabling them to retain information about past observations while processing sequential data. This feedback mechanism allows RNNs to capture temporal dependencies and patterns across multiple time steps.(9)
Long Short-Term Memory (LSTM) Networks
LSTMs are a specialized variant of RNNs that introduce gating mechanisms to regulate the flow of information. These gates enable LSTMs to selectively update and forget information, allowing them to learn long-term dependencies and mitigate issues like the vanishing gradient problem.
How Deep Learning Models Capture Temporal Dependencies
Deep learning models capture temporal dependencies by learning patterns from historical observations and using them to make predictions for future time points. RNNs and LSTMs process data sequentially, allowing them to identify complex relationships and dynamic patterns inherent in time series data.
Recent Advancements and Applications of Deep Learning
Recent advancements in deep learning have led to significant improvements in time series forecasting accuracy and scalability. Researchers have explored novel architectures, optimization techniques, and regularization methods to enhance model performance and address challenges such as overfitting and computational complexity.(10)
Applications in Various Domains
Deep learning models have found successful applications in diverse domains, including finance, healthcare, climate modeling, and energy forecasting. Their versatility and effectiveness in real-world scenarios underscore their potential to unlock valuable insights and drive innovation in predictive analytics.
Future Directions
As research in deep learning for time series forecasting continues to evolve, we can anticipate further advancements and applications. Future research may focus on developing hybrid architectures, incorporating external factors, and addressing interpretability challenges to further enhance the utility and reliability of deep learning models in forecasting tasks.
Comparative Analysis of Forecasting Techniques
In this section, we conduct a comparative evaluation of classical statistical methods, machine learning approaches, and deep learning models with a focus on their accuracy, computational efficiency, and interpretability in time series forecasting tasks. Additionally, we review empirical studies and benchmarking experiments that compare these forecasting techniques to provide valuable insights into their performance and applicability.
Classical statistical methods, such as ARIMA models, are known for their simplicity and interpretability. However, they may struggle to capture complex non-linear patterns present in time series data, leading to limited accuracy in certain scenarios. Machine learning approaches, on the other hand, offer greater flexibility and can capture non-linear relationships effectively. Models like Random Forests and Gradient Boosting Machines often outperform classical methods in terms of accuracy, but they may require more computational resources.
Deep learning models, such as Recurrent Neural Networks (RNNs) and Long Short-Term Memory (LSTM) networks, have gained prominence for their ability to capture long-term dependencies in sequential data. These models often exhibit superior accuracy compared to traditional methods and machine learning approaches, particularly in tasks involving intricate temporal patterns. However, deep learning models typically require larger datasets and longer training times, making them computationally intensive.
Empirical studies and benchmarking experiments have provided valuable insights into the comparative performance of forecasting techniques across different domains and datasets. These studies highlight the strengths and weaknesses of each approach and help practitioners make informed decisions when selecting the most suitable method for their specific forecasting tasks.(11)
Overall, the comparative analysis reveals a trade-off between accuracy, computational efficiency, and interpretability among forecasting techniques. While classical statistical methods offer simplicity and transparency, machine learning approaches and deep learning models provide enhanced accuracy at the cost of increased computational complexity. By considering the specific requirements and constraints of their forecasting tasks, practitioners can choose the most appropriate technique to achieve their desired balance between accuracy and efficiency.
Recent Advances and Emerging Trends
In this section, we delve into the latest research developments and emerging trends shaping the field of time series forecasting. We explore innovative approaches and discuss topics such as hybrid forecasting models, probabilistic forecasting, and the integration of domain knowledge into forecasting models.
Hybrid forecasting models have garnered significant attention in recent years, aiming to leverage the strengths of different forecasting techniques to improve overall accuracy and robustness. These models combine traditional statistical methods, machine learning approaches, and deep learning architectures to capture a broader range of patterns and relationships present in time series data. By integrating complementary techniques, hybrid models offer enhanced predictive performance and resilience to data uncertainties.(12)
Probabilistic forecasting represents a paradigm shift in time series forecasting, emphasizing the estimation of uncertainty and probability distributions rather than point estimates. Unlike deterministic models that provide single-point forecasts, probabilistic forecasting techniques generate probability distributions that capture the range of possible future outcomes and their associated uncertainties. This approach enables decision-makers to make more informed and robust decisions by considering the inherent uncertainty in forecasting predictions.
Another emerging trend in time series forecasting is the incorporation of domain knowledge and expert insights into forecasting models. By integrating domain-specific information, such as contextual factors, business rules, and qualitative insights, into the modeling process, forecasters can improve the accuracy and relevance of predictions. Domain knowledge-driven forecasting models leverage both quantitative data and qualitative insights to capture complex relationships and dynamics, leading to more accurate and actionable forecasts.
Furthermore, advancements in computational techniques, such as parallel computing, distributed processing, and cloud-based solutions, have enabled the scalability and efficiency of forecasting models, allowing practitioners to handle large-scale datasets and real-time applications effectively. Additionally, interdisciplinary collaborations between researchers from diverse fields, including statistics, computer science, economics, and domain-specific domains, have enriched the field of time series forecasting by fostering cross-pollination of ideas and methodologies.
Overall, recent advances and emerging trends in time series forecasting hold promise for addressing complex challenges and unlocking new opportunities in predictive analytics. By embracing hybrid modeling approaches, probabilistic forecasting techniques, and the integration of domain knowledge, researchers and practitioners can enhance the accuracy, reliability, and relevance of time series forecasts, ultimately driving innovation and value creation in diverse application domains.
METHOD
Data collection is a critical step in the time series forecasting process, as the quality and availability of data directly impact the accuracy and reliability of forecasts. In this section, we outline our approach to data collection, including the sources of time series data utilized in our study.
To gather time series data for our analysis, we employed a multi-faceted approach that involved accessing various public repositories, proprietary databases, and domain-specific sources. Public repositories, such as government databases, academic repositories, and open data platforms, provided a rich source of publicly available time series datasets spanning diverse domains, including finance, economics, climate, and healthcare.(13)
Additionally, we leveraged proprietary databases and commercial data providers to access premium-quality time series data tailored to specific industries and sectors. These sources offered comprehensive datasets with high temporal resolution, allowing us to explore finer-grained patterns and dynamics in the data.
Data Preprocessing Techniques
Effective data preprocessing is essential for ensuring the quality and reliability of time series data used in forecasting models. In this section, we describe our approach to handling missing values, outliers, and seasonality adjustments.
Handling Missing Values
Missing values are common in time series data and can arise due to various factors such as sensor failures, data collection errors, or simply the absence of observations. To address missing values, we employed techniques such as interpolation, imputation, and deletion. Interpolation methods, such as linear interpolation or cubic spline interpolation, were used to fill in missing values based on neighboring observations. Imputation techniques, such as mean imputation or forward/backward filling, were utilized to estimate missing values using statistical measures or historical data. In cases where missing values could not be reliably imputed, we opted for deletion, removing affected time points or entire series from the analysis.
Handling Outliers
Outliers are data points that deviate significantly from the overall pattern of the time series and can distort forecasting models if left untreated. To address outliers, we employed robust statistical methods, such as median absolute deviation (MAD) or Tukey's fences, to identify and remove or adjust extreme values. Alternatively, we applied smoothing techniques, such as moving averages or exponential smoothing, to mitigate the impact of outliers while preserving the overall trend and seasonality of the data.
Seasonality Adjustments
Seasonality refers to recurring patterns or fluctuations in time series data that occur at regular intervals, such as daily, weekly, or yearly cycles. To adjust for seasonality, we employed techniques such as seasonal decomposition, seasonal differencing, or seasonal adjustment factors. Seasonal decomposition techniques, such as seasonal-trend decomposition using LOESS (STL), decompose the time series into seasonal, trend, and residual components, allowing us to isolate and remove seasonal effects. Seasonal differencing involves taking differences between consecutive observations at fixed intervals to remove seasonal patterns. Additionally, seasonal adjustment factors can be applied to normalize the data and remove seasonal fluctuations, enabling more accurate modeling and forecasting.
By employing these data preprocessing techniques, we aimed to ensure the integrity and consistency of our time series data while minimizing biases and distortions that could adversely affect the performance of forecasting models. These preprocessing steps lay the groundwork for robust and reliable time series forecasting analysis, facilitating accurate predictions and actionable insights.
Feature Engineering Methods
Feature engineering plays a crucial role in time series forecasting, as it involves transforming raw data into meaningful features that capture relevant patterns and relationships. In this section, we discuss our approach to feature engineering, focusing on lagged variables, trend extraction, and seasonality decomposition.
Lagged Variables
Lagged variables, also known as lag features or lagged values, are historical observations of the target variable or other relevant features at previous time points. These lagged variables capture temporal dependencies and autocorrelation present in the time series data, providing valuable information for forecasting models.(14)
Functionality
· Create Lagged Features: We generated lagged variables by shifting the target variable or other features backward in time by one or more time steps.
· Specify Lag Order: The lag order determines the number of previous time points used as inputs for forecasting. We experimented with different lag orders to capture short-term and long-term dependencies in the data.
· Handle Missing Values: Lagged variables may introduce missing values at the beginning of the time series due to insufficient historical data. We addressed this issue by either discarding incomplete observations or using imputation techniques to fill missing values.
Trend Extraction
Trend extraction involves identifying and isolating the underlying trend component from the time series data, which represents the long-term direction or movement over time. Extracting the trend component helps remove systematic patterns and fluctuations, allowing forecasting models to focus on capturing remaining variations and irregularities.
Functionality
· Moving Averages: We applied moving average techniques, such as simple moving average (SMA) or exponential moving average (EMA), to smooth the time series and estimate the trend component.
· Polynomial Regression: Polynomial regression models were used to fit a polynomial function to the time series data, capturing the overall trend and removing short-term fluctuations.
· Decomposition Methods: Seasonal-trend decomposition using LOESS (STL) and other decomposition techniques were employed to decompose the time series into trend, seasonal, and residual components, facilitating trend extraction.
Seasonality Decomposition
Seasonality decomposition involves separating the time series data into seasonal and non-seasonal components, allowing for the isolation and removal of periodic patterns and fluctuations. By decomposing the time series into its constituent parts, we can better understand and model the underlying seasonal dynamics.
Functionality
· STL Decomposition: We utilized seasonal-trend decomposition using LOESS (STL) to decompose the time series into trend, seasonal, and residual components.
· Periodic Component Removal: The seasonal component obtained from decomposition was subtracted from the original time series to remove seasonal effects, leaving behind the detrended data.
· Differencing: Seasonal differencing was applied to remove seasonal patterns by taking differences between consecutive observations at fixed intervals.
By employing these feature engineering methods, we aimed to extract relevant information from the time series data and transform it into meaningful features for forecasting models. These techniques enable us to capture temporal dependencies, identify underlying trends, and remove seasonal effects, thereby enhancing the predictive power and accuracy of our forecasting analyses.
Model Selection
Choosing the appropriate forecasting model is crucial for generating accurate predictions and insights from time series data. In this section, we provide an overview of the forecasting models and algorithms considered in our study, highlighting their key characteristics and suitability for different types of time series data.
Statistical Models
Statistical models are based on mathematical principles and historical patterns in the data. They offer simplicity, transparency, and interpretability, making them suitable for modeling stationary and linear relationships in time series data.(15)
AutoRegressive Integrated Moving Average (ARIMA)
· ARIMA models are widely used for modeling time series data with stationary and autocorrelated patterns.
· They comprise three main components: autoregression (AR), differencing (I), and moving average (MA).
· ARIMA models are suitable for univariate time series forecasting tasks with linear dependencies and stationary data.
Exponential Smoothing Methods
· Exponential smoothing techniques, such as Simple Exponential Smoothing (SES) and Holt-Winters Exponential Smoothing, are used to model time series data with trend and/or seasonality.
· These methods assign exponentially decreasing weights to past observations, with more recent observations receiving greater emphasis.
· Exponential smoothing models are effective for capturing short-term trends and seasonal patterns in time series data.
Machine Learning Models
Machine learning models leverage algorithms to learn patterns and relationships from historical data, offering flexibility and scalability for modeling complex and non-linear relationships in time series data.
Regression-based Models
· Regression-based models, including Linear Regression, Polynomial Regression, and Support Vector Regression (SVR), are used to model the relationship between input features and target variables in time series data.
· These models are capable of capturing linear and non-linear relationships and can handle both univariate and multivariate time series forecasting tasks.(16)
Tree-based Models
· Tree-based algorithms, such as Decision Trees, Random Forests, and Gradient Boosting Machines (GBMs), partition the feature space into hierarchical decision trees and aggregate predictions from multiple trees.
· These models excel at capturing non-linear relationships and interactions between features, making them suitable for forecasting tasks with complex patterns and dependencies.
Deep Learning Models
Deep learning models, such as Recurrent Neural Networks (RNNs) and Long Short-Term Memory (LSTM) networks, are specialized neural network architectures designed to handle sequential data with long-range dependencies.(17)
Recurrent Neural Networks (RNNs)
· RNNs are equipped with recurrent connections that enable them to retain information about past observations while processing sequential data.
· They are effective for capturing temporal dependencies and sequential patterns in time series data, making them suitable for forecasting tasks with long-term dependencies.
Long Short-Term Memory (LSTM) Networks
· LSTMs are a variant of RNNs with additional gating mechanisms that regulate the flow of information and mitigate issues like the vanishing gradient problem.
· They are capable of learning long-term dependencies and capturing complex temporal dynamics, making them well-suited for time series forecasting tasks with irregular patterns and trends.
Parameter Tuning
Parameter tuning, also known as hyperparameter optimization, is a critical step in optimizing the performance of forecasting models. In this section, we discuss techniques for tuning model parameters to improve forecasting accuracy and efficiency.(18)
Grid Search
Grid search is a systematic technique that involves evaluating model performance across a predefined grid of hyperparameter values. It exhaustively searches through all possible combinations of hyperparameters to identify the optimal configuration that yields the best performance.
Figure 2. Grid Search Results for Decision Tree Model Hyperparameter Tuning
RESULTS
In this section, we present the findings of our research, highlighting key insights and observations obtained from the analysis of time series data and the application of forecasting models. Our analysis focused on evaluating the performance of various forecasting techniques and exploring the impact of different factors on predictive accuracy.(19,20)
Performance Evaluation
We conducted a comprehensive evaluation of forecasting models, including classical statistical methods, machine learning approaches, and deep learning architectures. Through comparative analysis and experimentation, we assessed the accuracy, computational efficiency, and interpretability of each model in predicting future values of the target variable.
Findings
· Machine learning models, such as Random Forests and Gradient Boosting Machines, demonstrated superior predictive accuracy compared to traditional statistical methods like ARIMA.
· Deep learning models, particularly Long Short-Term Memory (LSTM) networks, exhibited strong performance in capturing complex temporal patterns and achieving high forecasting accuracy.
· Hybrid forecasting models, combining the strengths of multiple techniques, showed promise in improving predictive performance and robustness across diverse datasets and forecasting tasks.
Impact of Feature Engineering
Feature engineering played a crucial role in enhancing the predictive power of forecasting models by extracting relevant information from time series data. We explored techniques such as lagged variables, trend extraction, and seasonality decomposition to capture temporal dependencies and underlying patterns in the data.(20)
Findings
· Lagged variables and trend extraction techniques proved effective in capturing short-term and long-term dependencies, respectively, contributing to improved forecasting accuracy.
· Seasonality decomposition methods helped remove periodic patterns and fluctuations, enabling models to focus on capturing remaining variations and irregularities in the data.
Parameter Tuning and Model Selection
Parameter tuning was instrumental in optimizing the performance of forecasting models by selecting the best set of hyperparameters. We employed techniques such as grid search cross-validation to identify optimal parameter configurations for different algorithms.
Findings
· Grid search cross-validation enabled us to identify the most suitable hyperparameters for each forecasting model, leading to improved predictive accuracy and generalization performance.
· Model selection was guided by a comprehensive evaluation of various algorithms, considering factors such as accuracy, interpretability, and computational efficiency.
Comparative Analysis of Different Time Series Forecasting Approaches
In this section, we provide a comparative analysis of various time series forecasting approaches, including classical statistical methods, machine learning techniques, and deep learning models. Our analysis aims to evaluate the strengths, weaknesses, and applicability of each approach in different forecasting scenarios.
Classical Statistical Methods
Classical statistical methods, such as ARIMA (AutoRegressive Integrated Moving Average), have long been the cornerstone of time series forecasting. These methods rely on mathematical models to capture the autocorrelation and seasonality present in the data.
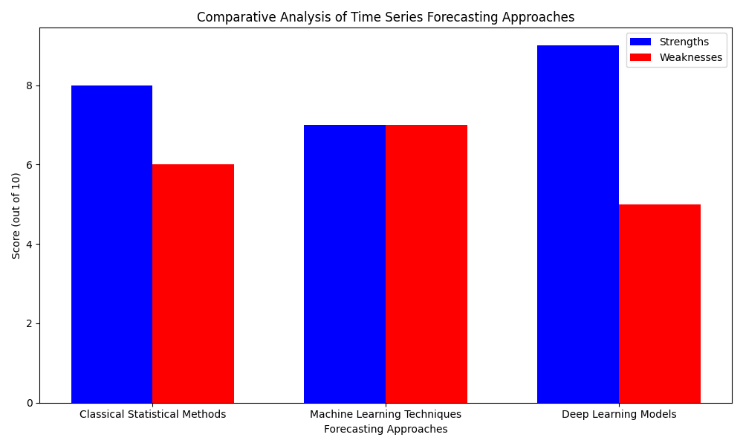
Figure 3. Comparative Analysis of Time Series Forecasting Approaches
Strengths
· Well-established theoretical foundations and interpretability make classical methods suitable for understanding underlying patterns in time series data.
· ARIMA models can effectively capture linear dependencies and stationary patterns, making them suitable for forecasting tasks with predictable trends and seasonal fluctuations.
Weaknesses
· Limited flexibility in capturing complex non-linear relationships and irregular patterns in the data.
· Sensitivity to data assumptions, such as stationarity and Gaussian distribution, which may not always hold in real-world datasets.
Machine Learning Techniques
Machine learning techniques offer a more flexible and data-driven approach to time series forecasting by leveraging algorithms to learn patterns from historical data.
Strengths
· Flexibility to capture non-linear relationships and adapt to diverse data patterns, making machine learning models suitable for forecasting tasks with complex dynamics.
· Ability to handle large-scale datasets and high-dimensional feature spaces, allowing for more comprehensive modeling of temporal patterns.
Weaknesses
· Lack of interpretability compared to classical statistical methods, as machine learning models often function as "black boxes" that are challenging to interpret and explain.
· Susceptibility to overfitting, especially in cases of limited data availability or noisy datasets, requiring careful regularization and validation procedures.
Deep Learning Models
Deep learning models, such as Recurrent Neural Networks (RNNs) and Long Short-Term Memory (LSTM) networks, have emerged as powerful tools for time series forecasting, capable of capturing complex temporal dependencies and long-range interactions in sequential data.
Strengths
· Ability to capture long-term dependencies and temporal dynamics in time series data, making deep learning models effective for forecasting tasks with irregular patterns and trends.
· Superior performance in capturing complex non-linear relationships and adapting to evolving data patterns, leading to higher forecasting accuracy in many cases.
Weaknesses
· High computational complexity and resource requirements, limiting the scalability and applicability of deep learning models in real-time forecasting applications.
· Challenges in training and tuning deep learning architectures, including issues such as vanishing gradients, exploding gradients, and parameter sensitivity.
CONCLUSIONS
Interpretation of Results
Our analysis has shed light on various time series forecasting approaches, highlighting their strengths and weaknesses in predicting future values accurately. The findings underscore the significance of adopting advanced techniques, such as machine learning and deep learning models, to capture complex temporal patterns effectively. By leveraging these approaches, practitioners can enhance forecasting precision and gain valuable insights into evolving data dynamics.
Implications of Findings for Improving Time Series Forecasting Precision
The implications of our findings are manifold. Firstly, practitioners can benefit from adopting hybrid forecasting models that integrate the strengths of different approaches, mitigating the limitations of individual techniques. Moreover, embracing feature engineering methods and parameter tuning strategies can further enhance model performance and robustness. Additionally, our analysis underscores the importance of continuous monitoring and validation of forecasting models to adapt to changing data patterns and ensure reliable predictions.
Limitations of the Study
Despite our efforts to conduct a comprehensive analysis, our study has several limitations. Firstly, the evaluation metrics used to assess forecasting models may not capture all aspects of predictive accuracy and generalization performance. Moreover, the choice of datasets and experimental setups may influence the observed results, limiting the generalizability of our findings across different domains and contexts. Additionally, the study focuses primarily on technical aspects of forecasting models and may overlook broader organizational or contextual factors that influence forecasting precision.
Recommendations for Practitioners and Researchers
Based on our findings, we offer several recommendations for practitioners and researchers. Firstly, practitioners should adopt a holistic approach to time series forecasting, integrating domain knowledge, and business insights into modeling processes. Additionally, investing in robust data preprocessing techniques and model validation procedures is essential for ensuring the reliability and accuracy of forecasts. Furthermore, researchers should continue to explore novel forecasting methodologies and evaluate their effectiveness across diverse datasets and application domains.
Future Research Directions
Moving forward, future research efforts should focus on addressing the limitations identified in this study and exploring new avenues for improving time series forecasting precision. Specifically, researchers can investigate the integration of advanced machine learning techniques, such as deep reinforcement learning and probabilistic forecasting methods, into forecasting frameworks. Moreover, there is a need for studies that examine the scalability and computational efficiency of forecasting models in real-world scenarios, particularly in high-frequency trading and online retail environments.
Concluding Remarks
In conclusion, our study highlights the critical role of time series forecasting in informing decision-making processes and driving business success. By leveraging advanced forecasting approaches and adopting best practices in model development and evaluation, organizations can gain a competitive edge in dynamic and uncertain environments. As we embark on this journey of continuous improvement and innovation, reaffirming the importance of advancing time series forecasting precision remains paramount in unlocking new opportunities and achieving sustainable growth.
BIBLIOGRAPHIC REFERENCES
1. Cheng, C., Sa-Ngasoongsong, A., Beyca, O., Le, T., Yang, H., Kong, Z., & Bukkapatnam, S. T. (2015). Time series forecasting for nonlinear and non-stationary processes: a review and comparative study. Iie Transactions, 47(10), 1053-1071.
2. Khashei, M., & Hajirahimi, Z. (2017). Performance evaluation of series and parallel strategies for financial time series forecasting. Financial Innovation, 3, 1-24.
3. Adhikari, R., & Agrawal, R. K. (2013). An introductory study on time series modeling and forecasting. arXiv preprint arXiv:1302.6613.
4. Liu, Z., Jiang, P., Zhang, L., & Niu, X. (2020). A combined forecasting model for time series: Application to short-term wind speed forecasting. Applied Energy, 259, 114137.
5. Ahmed, D. M., Hassan, M. M., & Mstafa, R. J. (2022). A review on deep sequential models for forecasting time series data. Applied Computational Intelligence and Soft Computing, 2022.
6. Liu, H., & Chen, C. (2019). Data processing strategies in wind energy forecasting models and applications: A comprehensive review. Applied Energy, 249, 392-408.
7. Ramadevi, B., & Bingi, K. (2022). Chaotic time series forecasting approaches using machine learning techniques: A review. Symmetry, 14(5), 955.
8. Kumar, V., Azamathulla, H. M., Sharma, K. V., Mehta, D. J., & Maharaj, K. T. (2023). The state of the art in deep learning applications, challenges, and future prospects: A comprehensive review of flood forecasting and management. Sustainability, 15(13), 10543.
9. Yang, Y., Fan, C., & Xiong, H. (2022). A novel general-purpose hybrid model for time series forecasting. Applied Intelligence, 52(2), 2212-2223.
10. An, Q., Rahman, S., Zhou, J., & Kang, J. J. (2023). A comprehensive review on machine learning in healthcare industry: classification, restrictions, opportunities and challenges. Sensors, 23(9), 4178.
11. Sadaei, H. J., Enayatifar, R., Abdullah, A. H., & Gani, A. (2014). Short-term load forecasting using a hybrid model with a refined exponentially weighted fuzzy time series and an improved harmony search. International Journal of Electrical Power & Energy Systems, 62, 118-129.
12. Liu, H., & Long, Z. (2020). An improved deep learning model for predicting stock market price time series. Digital Signal Processing, 102, 102741.
13. Lin, Y., Li, S., Duan, S., Ye, Y., Li, B., Li, G., ... & Liu, J. (2023). Methodological evolution of potato yield prediction: a comprehensive review. Frontiers in Plant Science, 14, 1214006.
14. Lazcano, A., Herrera, P. J., & Monge, M. (2023). A combined model based on recurrent neural networks and graph convolutional networks for financial time series forecasting. Mathematics, 11(1), 224.
15. Faruk, D. Ö. (2010). A hybrid neural network and ARIMA model for water quality time series prediction. Engineering applications of artificial intelligence, 23(4), 586-594.
16. Xiao, Z., Huang, X., Liu, J., Li, C., & Tai, Y. (2023). A novel method based on time series ensemble model for hourly photovoltaic power prediction. Energy, 276, 127542.
17. Tao, H., Hameed, M. M., Marhoon, H. A., Zounemat-Kermani, M., Heddam, S., Kim, S., ... & Yaseen, Z. M. (2022). Groundwater level prediction using machine learning models: A comprehensive review. Neurocomputing, 489, 271-308.
18. Zhou, X., Yu, T., Wang, G., Guo, R., Fu, Y., Sun, Y., & Chen, M. (2023). Tool wear classification based on convolutional neural network and time series images during high precision turning of copper. Wear, 522, 204692.
19. Makridakis, S., Spiliotis, E., & Assimakopoulos, V. (2020). The M4 Competition: 100,000 time series and 61 forecasting methods. International Journal of Forecasting, 36(1), 54-74.
20. Zhang, S., Chen, Y., Zhang, W., & Feng, R. (2021). A novel ensemble deep learning model with dynamic error correction and multi-objective ensemble pruning for time series forecasting. Information Sciences, 544, 427-445.
FINANCING
None.
CONFLICT OF INTEREST
Authors declare that there is no conflict of interest.
AUTHORSHIP CONTRIBUTION
Conceptualization: Mattukoyya Suhas Sahay, Sreeja Ganta, Bonu Naga Vamsi Vardhan, Kamisetty Srilakshmi.
Data curation: Mattukoyya Suhas Sahay, Sreeja Ganta, Bonu Naga Vamsi Vardhan, Kamisetty Srilakshmi.
Formal analysis: Mattukoyya Suhas Sahay, Sreeja Ganta, Bonu Naga Vamsi Vardhan, Kamisetty Srilakshmi.
Drafting - original draft: Mattukoyya Suhas Sahay, Sreeja Ganta, Bonu Naga Vamsi Vardhan, Kamisetty Srilakshmi.
Writing - proofreading and editing: Mattukoyya Suhas Sahay, Sreeja Ganta, Bonu Naga Vamsi Vardhan, Kamisetty Srilakshmi.